El comportamiento asintótico de una función f(n) se refiere al crecimiento de f(n) a medida que n crece.

Por lo general, ignoramos los valores pequeños de n , ya que generalmente estamos interesados ​​en estimar qué tan lento será el programa en entradas grandes (cuando n tiende a infinito).

Una buena regla general es que cuanto más lenta sea la tasa de crecimiento asintótico, mejor será el algoritmo. Aunque no siempre es cierto.

Por ejemplo, un algoritmo lineal $ f (n) = d * n + k $ siempre es asintóticamente mejor que uno cuadrático, $ f (n) = cn ^ 2 + q $.

¿Por qué analizar el rendimiento?

Hay muchas cosas importantes que deben tenerse en cuenta, como la facilidad de uso, la modularidad, la seguridad, la capacidad de mantenimiento, etc. ¿Por qué preocuparse por el rendimiento?
La respuesta es simple, podemos tener todas las cosas anteriores solo si tenemos rendimiento. Entonces, el rendimiento es como la moneda a través de la cual podemos comprar todas las cosas anteriores.

Dados dos algoritmos para una tarea, ¿cómo descubrimos cuál es mejor?
Una forma ingenua de hacer esto es: implementar ambos algoritmos y ejecutar los dos programas en su computadora para diferentes entradas y ver cuál toma menos tiempo. Hay muchos problemas con este enfoque para el análisis de algoritmos.

1. Es posible que para algunas entradas, el primer algoritmo funcione mejor que el segundo. Y para algunas entradas, el segundo funciona mejor.
2. También podría ser posible que para algunas entradas, el primer algoritmo funcione mejor en una máquina y el segundo funcione mejor en otra máquina para algunas otras entradas.

El análisis asintótico es la gran idea que maneja los problemas anteriores al analizar algoritmos. En el análisis asintótico, evaluamos el rendimiento de un algoritmo en términos de tamaño de entrada (no medimos el tiempo de ejecución real). Calculamos cómo aumenta el tiempo (o espacio) que toma un algoritmo con el tamaño de entrada.
Por ejemplo, consideremos el problema de búsqueda (búsqueda de un elemento determinado) en una matriz ordenada. Una forma de buscar es la búsqueda lineal (el orden de crecimiento es lineal) y la otra es la búsqueda binaria (el orden de crecimiento es logarítmico). Para entender cómo el análisis asintótico resuelve los problemas mencionados anteriormente al analizar algoritmos, digamos que ejecutamos la búsqueda lineal en una computadora rápida y la búsqueda binaria en una computadora lenta. Para valores pequeños de tamaño de matriz de entrada n, la computadora rápida puede tomar menos tiempo. Pero, después de cierto valor del tamaño de la matriz de entrada, la búsqueda binaria definitivamente comenzará a tomar menos tiempo en comparación con la búsqueda lineal a pesar de que la búsqueda binaria se ejecuta en una máquina lenta. La razón es el orden de crecimiento de la búsqueda binaria con respecto al tamaño de entrada logarítmico, mientras que el orden de crecimiento de la búsqueda lineal es lineal. Por lo tanto, las constantes dependientes de la máquina siempre se pueden ignorar después de ciertos valores de tamaño de entrada

El Principio de Invarianza nos permite deducir que no existe una unidad que se deba utilizar para expresar la eficiencia teórica de un algoritmo. En su lugar, expresaremos solamente el tiempo requerido por el algoritmo, salvo una constante multiplicativa.
Por este principio, todas las implementaciones de un mismo algoritmo tienen las mismas características, aunque la constante multiplicativa pueda cambiar de una implementación a otra.

 

¿El análisis asintótico siempre funciona?

El análisis asintótico no es perfecto, pero esa es la mejor manera disponible para analizar algoritmos. Por ejemplo, supongamos que hay dos algoritmos de clasificación que toman 1000 n Log n y 2n Log n, respectivamente, en una máquina. Ambos algoritmos son asintóticamente iguales (el orden de crecimiento es n Log n). Entonces, con el análisis asintótico, no podemos juzgar cuál es mejor ya que ignoramos las constantes en el análisis asintótico.
Además, en el análisis asintótico, siempre hablamos de tamaños de entrada mayores que un valor constante. Es posible que esas entradas grandes nunca se le den a su software y que un algoritmo que sea asintóticamente más lento, siempre funcione mejor para su situación particular. Por lo tanto, es posible que se de algún caso raro en particular en el que termine eligiendo un algoritmo que sea asintóticamente más lento pero más rápido para su software.

Notaciones

Las notaciones asintóticas se usan para describir el comportamiento de una función en el límite, cuando el argumento tiende hacia un valor particular (a menudo infinito), generalmente en términos de funciones más simples. En la teoría de la complejidad computacional, la notación Big O (O grande) es de uso común para clasificar los algoritmos según cómo responden (por ejemplo, en sus requisitos de tiempo de procesamiento o espacio de trabajo) a los cambios en el tamaño de entrada.

Una familia de funciones que comparten el mismo comportamiento asintótico será llamada un Orden de complejidad.

En matemática, la Notación de Landau, también llamada «o minúscula» y «O mayúscula», es una notación para la comparación asintótica de funciones, lo que permite establecer la cota inferior asintótica, la cota superior asintótica y la cota ajustada asintótica.

El análisis en si consiste en comparar la función del comportamiento de nuestro algoritmo con funciones «patrón», como ser:

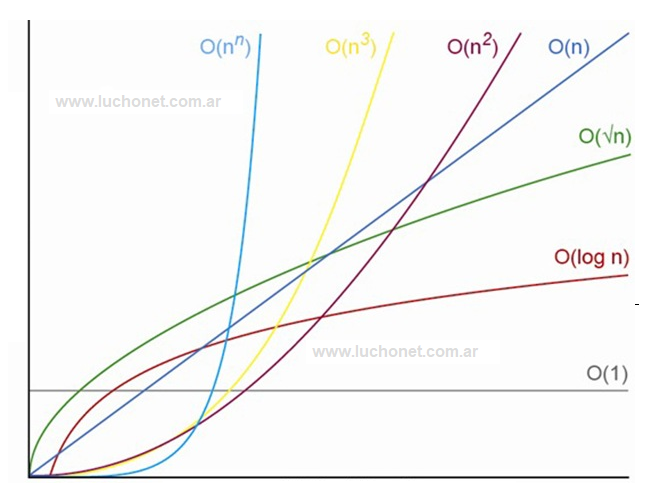
O(1): Complejidad constante. Cuando las instrucciones se ejecutan una vez.

O(log n): Complejidad logarítmica. Esta suele aparecer en determinados algoritmos con iteración o recursión no estructural, ejemplo la búsqueda binaria.

O(n): Complejidad lineal. Es una complejidad buena y también muy usual. Aparece en la evaluación de bucles simples siempre que la complejidad de las instrucciones interiores sea constante.

O(n log n): Complejidad cuasi-lineal. Se encuentra en algoritmos de tipo divide y vencerás como por ejemplo en el método de ordenación quicksort y se considera una buena complejidad. Si n se duplica, el tiempo de ejecución es ligeramente  mayor del doble.

O(n²): Complejidad cuadrática. Aparece en bucles o ciclos doblemente anidados.  Si n se duplica, el tiempo de ejecución aumenta cuatro veces. O(n^3): Complejidad cúbica. Suele darse en bucles con triple anidación. Si n se duplica, el tiempo de ejecución se multiplica por ocho. Para un valor grande de n empieza a crecer dramáticamente.

O(n^p): Complejidad polinómica (a > 3). Si a crece, la complejidad del programa  es bastante mala.

O(cⁿ): Complejidad exponencial. No son útiles en la práctica por el elevadísimo tiempo de ejecución. Se dan en subprogramas recursivos que  contengan dos o más llamadas internas.

En pos de caracterizar los algoritmos y tomando en cuenta las notaciones surgen los siguientes análisis:

• Análisis de cota superior asintótica
• Análisis de cota inferior asintótica
• Análisis de cota ajustada asintótica