La complejidad algorítmica es una medida que evalúa el orden del recuento de operaciones , realizado por un determinado algoritmo o en función del tamaño de los datos de entrada. Para poner esto más simple, la complejidad es una aproximación aproximada del número de pasos necesarios para ejecutar un algoritmo. Cuando evaluamos la complejidad, hablamos del recuento del orden de operación, no del recuento exacto. Por ejemplo, si tenemos un orden de operaciones de N ² para procesar N elementos, entonces N 2/2 y 3 * N ² son del mismo orden cuadrático.

Pero en términos generales sabemos que existen problemas más difíciles de resolver que otros. E indicar que un problema es más difícil que otro hace referencia a la cantidad de recursos (tiempo de ejecución o memoria) que son necesarios para alcanzar dicha solución, suponiendo la solución exista. Es decir que está relacionado al consumo del algoritmo y no a la naturaleza o estructura lógica del algoritmo.

La Teoría de la Complejidad Computacional es la rama de las Ciencias de la Computación que estudia y clasifica a los problemas de acuerdo a su complejidad inherente. La medición de la complejidad se realiza con técnicas propias del análisis de algoritmos, que por lo tanto constituye una disciplina relacionada con la Teoría de la Complejidad, aunque sus objetivos son diferentes.  Es decir, el análisis de algoritmos busca determinar la cantidad de recursos que emplea un algoritmo, mientras que la Teoría de la Complejidad intenta caracterizar a todos los posibles algoritmos para resolver un problema dado (específicamente, determinar qué problemas pueden o no ser resueltos empleando una cierta cantidad limitada de recursos).

Mas allá de de su complejidad y sus clasificaciones, es importante hacer la distinción entre tipos de problemas. Clasificándolos por objetivo a cumplir identificamos al menos en tres tipos:

• Problemas de decisión: son aquellos que sólo admiten como resultado un valor de veracidad (true o false, sí o no). Un ejemplo de este tipo de problemas sería este planteo: dado el conjunto de N ciudades ¿existe la forma de recorrerlas a todas sin pasar dos veces por la misma ciudad? Otro ejemplo sería, dados dos números x e y , ¿divide x equitativamente y ?Los problemas de decisión suelen aparecer en cuestiones matemáticas de capacidad de decisión , es decir, la cuestión de la existencia de un método eficaz para determinar la existencia de algún objeto o su pertenencia a un conjunto; Algunos de los problemas más importantes en matemáticas son indecidibles .
• Problemas funcionales o «Function problems» (búsqueda de resultados): son aquellos que proponen encontrar una solución específica (si existe) para el planteo dado. Ejemplos de problemas de búsqueda son: hallar las raíces de una ecuación de segundo grado dados los coeficientes de la misma, dados n números, obtener el promedio de esos números, etc.Los problemas de decisión están estrechamente relacionados con problemas de funcionales, aunque que pueden tener respuestas que son más complejas que un simple «sí» o «no». Un problema funcional podría ser «dados dos números x e y , ¿cuál es x dividido por y ?».Cada problema funcional puede convertirse en un problema de decisión y cada problema de decisión puede convertirse en el problema funcional, al calcular la función característica del conjunto asociado al problema de decisión. Si esta función es computable, entonces el problema de decisión asociado es decidible.
•  Problemas de optimización: A diferencia de los problemas de decisión, para los cuales solo hay una respuesta correcta para cada entrada, los problemas de optimización tienen que ver con encontrar la mejor respuesta para una entrada en particular. Los problemas de optimización surgen naturalmente en muchas aplicaciones, como el problema del vendedor ambulante y muchas preguntas en la programación lineal .Existen técnicas estándar para transformar los problemas de función y optimización en problemas de decisión. Por ejemplo, en el problema del vendedor ambulante, el problema de optimización es producir un recorrido con un peso mínimo. El problema de decisión asociado es: para cada N , decidir si el gráfico tiene algún recorrido con un peso inferior a N. Al responder repetidamente el problema de decisión, es posible encontrar el peso mínimo de un recorrido.Debido a que la teoría de los problemas de decisión está muy bien desarrollada, la investigación en teoría de la complejidad se ha centrado típicamente en los problemas de decisión. Los problemas de optimización en sí mismos siguen siendo interesantes en la teoría de la computabilidad, así como en campos como la investigación de operaciones

 

Reducción de complejidad

En la teoría de la complejidad computacional , una reducción es un algoritmo para transformar un problema en otro problema. Se puede usar una reducción suficientemente eficiente de un problema a otro para mostrar que el segundo problema es al menos tan difícil como el primero.

Intuitivamente, el problema A es reducible al problema B si un algoritmo para resolver el problema B de manera eficiente (si existiera) también podría usarse como una subrutina para resolver el problema A de manera eficiente. Cuando esto es cierto, resolver A no puede ser más difícil que resolver B. «Más difícil» significa tener una estimación más alta de los recursos computacionales requeridos en un contexto dado (por ejemplo, mayor complejidad de tiempo , mayor requisito de memoria, necesidad costosa de núcleos de procesador de hardware adicionales una solución paralela en comparación con una solución de un solo hilo, etc.).

Escribimos A\leq _{m}B , generalmente con un subíndice en ≤ para indicar el tipo de reducción que se está utilizando (m: reducción de mapeo , p: reducción polinómica ).

La estructura matemática generada en un conjunto de problemas por las reducciones de un tipo particular generalmente forma un preorden , cuyas clases de equivalencia pueden usarse para definir grados de clases de insolubilidad y complejidad .

 Hay dos situaciones principales en las que necesitamos usar reducciones:

• Nos encontramos tratando de resolver un problema que es similar a un problema que ya hemos resuelto. En estos casos, a menudo una forma rápida de resolver el nuevo problema es transformar cada instancia del nuevo problema en instancias del problema anterior, resolverlas usando nuestra solución existente y luego usarlas para obtener nuestra solución final. Este es quizás el uso más obvio de las reducciones.
• Y el segundo caso, supongamos que tenemos un problema que hemos demostrado que es difícil de resolver y que tenemos un problema nuevo similar. Podríamos sospechar que también es difícil de resolver. Argumentamos por contradicción: supongamos que el nuevo problema es fácil de resolver; entonces, si podemos demostrar que cada instancia del viejo problema puede resolverse fácilmente transformándola en instancias del nuevo problema y resolviendo eso, tenemos una contradicción. Esto establece que el nuevo problema también es difícil.

Un ejemplo muy simple de una reducción es desde la multiplicación hasta elevar al cuadrado. Supongamos que todo lo que sabemos hacer es sumar, restar, tomar cuadrados y dividir por dos. Podemos usar este conocimiento, combinado con la siguiente fórmula, para obtener el producto de dos números:

a . b =\frac{\left (\left ( a+b \right )^{2}-a^{2}-b^{2} \right )}{a}

También tenemos una reducción en la otra dirección; obviamente, si podemos multiplicar dos números, podemos elevar al cuadrado un número. Esto parece implicar que estos dos problemas son igualmente difíciles. Este tipo de reducción corresponde a la reducción de Turing .

Sin embargo, la reducción se vuelve mucho más difícil si agregamos la restricción de que solo podemos usar la función de elevar al cuadrado una vez, y solo al final. En este caso, incluso si se nos permite usar todas las operaciones aritméticas básicas, incluida la multiplicación, no existe reducción en general, porque para obtener el resultado deseado como un cuadrado, primero tenemos que calcular su raíz cuadrada, y esta raíz cuadrada podría ser un número irracional como \sqrt{2}, y eso no puede ser construido por operaciones aritméticas en números racionales. Sin embargo, yendo en la otra dirección, ciertamente podemos elevar al cuadrado un número con una sola multiplicación, solo al final. Usando esta forma limitada de reducción, hemos demostrado el sorprendente resultado de que la multiplicación es más difícil en general que la potencia de 2. Esto corresponde a una reducción de muchos.

Una reducción es un pedido previo , que es una relación reflexiva y transitiva , en P (N) × P(N), donde P(N) es el conjunto de potencia de los números naturales .

Clases de complejidad

La teoría de la complejidad estudia y clasifica problemas de acuerdo a su complejidad interna inherente dando como resultado el planteado diversos conjuntos de problemas, agrupados según lo que se sabe de ellos en cuanto a consumo de recursos y posibilidades de ser resueltos con diversos tipos de máquinas (teóricas o concretas).
Estos conjuntos de problemas similares se denominan «clases de complejidad» .
La clase mas simple y a su vez mas importante de la teoría de la complejidad es la clase de complejidad P (o simplemente, clase P, abreviatura de Polynomial-Time), definiéndose como:

• Clase P: Conjunto de todos los problemas de decisión que pueden ser resueltos con algoritmos de tiempo polinomial usando una máquina determinista.

La definición hace referencia específicamente a problemas de decisión (problemas con salida verdadero o falso), pero no problema extrapolarlo a problemas de otros tipos. Las bases y fundamentos esenciales de la teoría de la complejidad se basan en problemas de decisión, pero sus conclusiones son aplicables a otros tipos de problemas contenidos en otras clases de complejidad. Un ejemplo de ello es la clase FP que es similar a P, sin la restricción de que sean problemas de decisión. Cuando se habla de tiempo polinomial, se da sentado que se hace referencia a que el tiempo de ejecución del algoritmo es una función polinómica del tamaño de la entrada para ese algoritmo.
La clase P es en realidad el conjunto de todos los problemas para los cuales se conocen soluciones consideradas eficientes, o al menos aceptables (desde el punto de vista del tiempo de ejecución en una máquina determinista). Se dice que P es la clase en la que desearíamos que esté cualquier problema, debido a que un problema en P tiene al menos una solución conocida y «eficiente» . Es decir que pertenecen a P problemas tales como el ordenamiento de un arreglo (existen algoritmos de ordenamiento que ejecutan en tiempo polinomial), o la búsqueda de un elemento en un arreglo o una lista. La clase P entonces, agrupa problemas que hemos identificado como fáciles de resolver.
Sin embargo, existen muchos otros problemas para los cuales simplemente no se conocen soluciones que puedan correr en un tiempo de ejecución razonable; es decir que para muchos problemas existen algoritmos conocidos, pero esos algoritmos (normalmente basados en estrategia de fuerza bruta) con tiempos de ejecución exponencial, resultando muy ineficientes  independientemente de la tecnología de la computadora en la que se implemente, y aún para tamaños relativamente pequeños del conjunto de datos a procesar. Algunos problemas muy estudiados que tienen estas características, como por ejemplo el Problema del Viajante (dadas n ciudades y el conjunto de rutas que permiten vincularlas, se debe calcular el recorrido más corto que permita, saliendo de alguna de ellas, visitar a todas las otras, sin repetir ciudad alguna); el Problema de Clique Máximo, etc.

Podríamos considerar que todo problema que no esté en P podría clasificarse en otra clase «No-P», pero esa afirmación es errónea ya que el hecho de que un problema X no pertenezca a P, en realidad nos está diciendo que no se conocen soluciones de tiempo polinomial para el problema X , y no nos dice nada respecto de posibles buenas soluciones para X aún no encontradas.
Tanto el problema del viajante como el de clique máximo no pertenecen a P (hasta el momento no se ha encontrado una solución en P), pero cabe aclarar de que para ambos existen algoritmos que ejecutarían en tiempo polinomial en una máquina no determinista (y dentro de la teoría de la complejidad es irrelevante si las máquinas son no deterministas o no).
Es por ello y en forma más ajustada que la teoría de la complejidad plantea la clase de complejidad NP (o simplemente, clase NP que viene de Nondeterministic Polynomial-Time) :

• Clase NP: Conjunto de todos los problemas de decisión que pueden ser resueltos con algoritmos de tiempo polinomial usando una máquina no determinista.

Sigue involucrando problemas de decisión pero como vimos, no hay problemas de extrapolar.
La clase NP abarca problemas de decisión que en una máquina determinista requerirían tiempo exponencial, pero que en una máquina no determinista insumirían tiempo polinomial. Eel problema del viajante y el del clique máximo pertenecen a NP.

Es decir que se puede clasificar basándose en el tipo de maquina que resuelve el problema (determinista y no determinista). También deducimos de ello que existen problemas que no estarían contenidos ni en P ni en NP, por lo tanto se necesitan otras clases de complejidad para clasificar a estos problemas. Y por esto surgen otras dos clasificaciones:

• Clase EXP: Conjunto de todos los problemas de decisión que pueden ser resueltos con algoritmos de tiempo exponencial usando una máquina determinista. El nombre proviene de Exponencial-Time.
• Clase NEXP: Conjunto de todos los problemas de decisión que pueden ser resueltos con algoritmos de tiempo exponencial usando una máquina no determinista. El nombre proviene de Nondeterministic Exponential-Time.

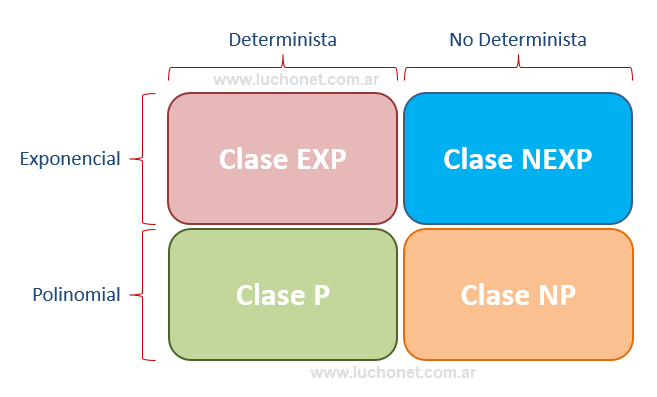
Si tomamos en cuenta el tiempo de ejecución y el tipo de máquina, podemos resumirlo en el siguiente cuadro:

Un mismo problema puede ser clasificado en dos o más clases diferentes de complejidad. Todos los problemas que están en P, también están en NP; es decir que si una máquina determinista puede resolver un problema en tiempo polinomial, es completamente obvio que una máquina no determinista también puede hacerlo. Por lo tanto, P es un subconjunto de NP ( P ⊂ NP). Razonamientos similares (que dejamos para ser verificados por el estudiante) llevan a concluir que:

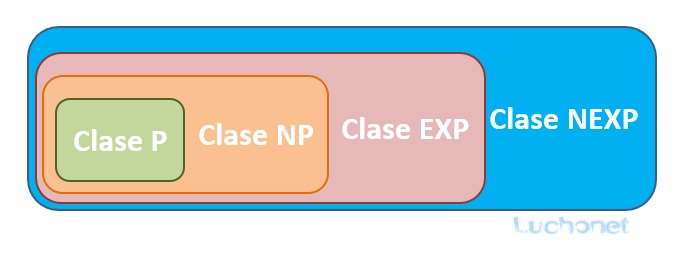
P ⊂ NP ⊂ EXP ⊂ NEXP

Pasándolos a un cuadro quedarían contenidos así:

Existe otra clase de complejidad llamada NPC o NP Completo. Un problema es NP completo cuando puede resolverse mediante una clase restringida de algoritmos de búsqueda de fuerza bruta y puede usarse para simular cualquier otro problema con un algoritmo similar. Más precisamente, cada entrada al problema debe asociarse con un conjunto de soluciones de longitud polinómica, cuya validez se puede probar rápidamente (en tiempo polinómico), de modo que la salida para cualquier entrada sea «sí», si la solución se establece no está vacío y «no», si está vacío. La clase de complejidad de los problemas de esta forma se llama NP , una abreviatura de «tiempo polinomial no determinista «. Se dice que un problema es NP-hard si todo en NP puede transformarse en tiempo polinómico en él, y un problema es NP-completo si está en NP y NP-hard. Los problemas NP-completos representan los problemas más difíciles en NP. Si algún problema de NP completo tiene un algoritmo de tiempo polinómico, todos los problemas en NP sí. El conjunto de problemas NP-completos a menudo se denota por NP-C o NPC .

Aunque una solución a un problema de NP-completo se puede verificar «rápidamente», no se conoce una forma de encontrar una solución rápidamente. Es decir, el tiempo requerido para resolver el problema usando cualquier algoritmo conocido actualmente aumenta rápidamente a medida que crece el tamaño del problema. Como consecuencia, determinar si es posible resolver estos problemas rápidamente, llamado el problema P versus NP , es uno de los problemas fundamentales no resueltos en la informática actual.

Si bien un método para calcular las soluciones a los problemas de NP completo permanece rápidamente sin descubrir, los informáticos y programadores con frecuencia aún encuentran problemas de NP completo. Los problemas de NP completo a menudo se abordan mediante el uso de métodos heurísticos y algoritmos de aproximación .

El concepto de «NP-completo» fue introducido por Stephen Cook en un artículo titulado «The complexity of theorem-proving procedures» en las páginas 151-158 de Proceedings of the 3rd Annual ACM Symposium on Theory of Computing en 1971, aunque el término «NP-completo» como tal no aparece en el documento. En la conferencia de ciencias de la computación hubo un intenso debate entre los científicos de la computación sobre si los problemas NP-completos podían ser resueltos en tiempo polinómico o en una máquina de Turing determinista. John Hopcroft llevó a todos los asistentes de la conferencia a consenso concluyendo que el estudio sobre si los problemas NP-completos son resolubles en tiempo polinómico debería ser pospuesto ya que nadie había conseguido probar formalmente sus hipótesis ni en un sentido ni en otro. Esto se conoce como el problema ¿P=NP?.

El Teorema de Cook demuestra que el problema de satisfacibilidad booleana es un problema NP-completo. En 1972, Richard Karp demostró que otros problemas eran también NP-completos. A partir de los resultados originales del Teorema de Cook, se han descubierto cientos de problemas que también pertenecen a NP-completo mediante reducciones desde otros problemas que previamente se habían demostrado NP-completos; muchos de estos problemas han sido recogidos en libro de 1979 de Garey and Johnson’s Computers and Intractability: A Guide to NP-Completeness.

P vs. NP

El problema P versus NP es un gran problema no resuelto en informática. Pregunta si cada problema cuya solución puede verificarse rápidamente (técnicamente, verificada en tiempo polinomial) también puede resolverse rápidamente (nuevamente, en tiempo polinomial).

Es uno de los siete problemas del Premio del Milenio seleccionados por el Clay Mathematics Institute, cada uno de los cuales tiene un premio de US $ 1,000,000 para la primera solución correcta.

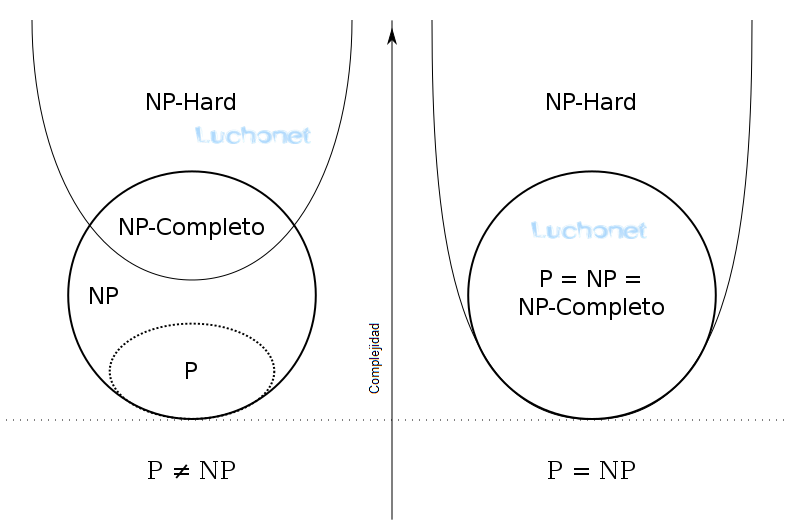
Una respuesta a la pregunta P = NP determinaría si los problemas que pueden verificarse en el tiempo polinómico también pueden resolverse en el tiempo polinómico. Si resultara que P ≠ NP, que se cree ampliamente, significaría que hay problemas en NP que son más difíciles de calcular que verificar: no podrían resolverse en tiempo polinómico, pero la respuesta podría verificarse en tiempo polinómico .

Si se demostrase que P = NP (los problemas que pueden verificarse en el tiempo polinómico también pueden resolverse en el tiempo polinómico), implicaría que cualquier máquina determinista es al menos tan poderosa como una no determinista y sólo se necesitaría encontrar el algoritmo correcto. También implicaría que muchas de las clases de la teoría son equivalentes entre sí, simplificándose la teoría de forma notable.

Ahora si se demostrase que P ≠ NP, se confirmaría que el no determinismo es una herramienta potente. Y por ello, se dejaría de buscar una solución eficiente para muchos problemas hoy considerados intratables, enfocándose en resolver esos problemas en base a soluciones aproximadas o sub-óptimas .

Además de ser un problema importante en la teoría computacional, una prueba de cualquier manera tendría profundas implicaciones para las matemáticas, la criptografía, la investigación de algoritmos, la inteligencia artificial, la teoría de juegos, el procesamiento multimedia, la filosofía, la economía y muchos otros campos. En 2010, el matemático Jeffrey Lagarias comentó que este problema es «extraordinariamente difícil» y «completamente fuera del alcance» de las matemáticas actuales.

Tratabilidad 

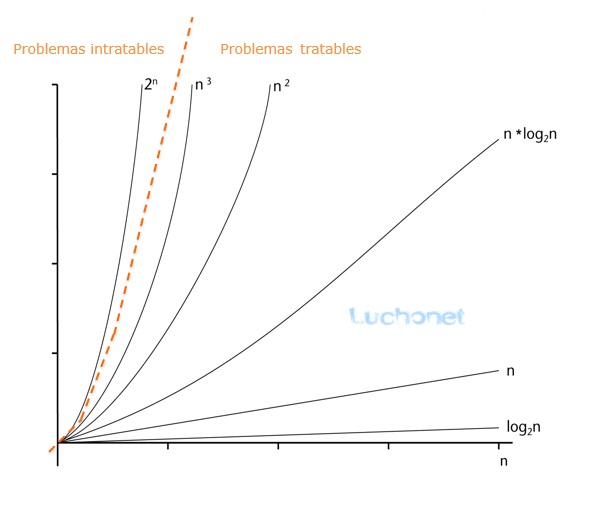
Un problema que puede resolverse en teoría (por ejemplo, con recursos grandes pero limitados, especialmente tiempo), pero para el cual en la práctica cualquier solución requiere demasiados recursos para ser útil, se conoce como un problema intratable (intractable en ingles).  Por el contrario, un problema que se puede resolver en la práctica se llama un problema tratable (tractable en ingles), literalmente «un problema que se puede manejar». El término inviable (infeasible en inglés) (literalmente «no se puede hacer») a veces se usa indistintamente con intratable, aunque esto corre el riesgo de confusión con una solución factible en la optimización matemática.

Los problemas tratables se identifican frecuentemente con problemas que tienen soluciones de tiempo polinómico (P, PTIME); Esto se conoce como la tesis de Cobham-Edmonds. Los problemas que se sabe que son intratables en este sentido incluyen aquellos que son DIFÍCILES. Si NP no es lo mismo que P, entonces los problemas NP-duros también son intratables en este sentido.

Sin embargo, esta identificación es inexacta: una solución de tiempo polinomial con un alto grado o un coeficiente principal grande crece rápidamente y puede ser poco práctico para problemas prácticos de tamaño; Por el contrario, una solución de tiempo exponencial que crece lentamente puede ser práctica con aportes realistas, o una solución que lleva mucho tiempo en el peor de los casos puede llevar poco tiempo en la mayoría de los casos o en el caso promedio, y por lo tanto aún es práctica. Decir que un problema no está en P no implica que todos los casos grandes del problema sean difíciles o incluso que la mayoría de ellos lo sean. Por ejemplo, se ha demostrado que el problema de decisión en la aritmética de Presburger no está en P, aunque se han escrito algoritmos que resuelven el problema en tiempos razonables en la mayoría de los casos. Del mismo modo, los algoritmos pueden resolver el problema de la mochila(knapsack) NP completo en un amplio rango de tamaños en menos de un tiempo cuadrático y los solucionadores SAT manejan rutinariamente grandes instancias del problema de satisfacción booleana completa NP.

Para ver por qué los algoritmos de tiempo exponencial generalmente no se pueden usar en la práctica, considere un programa que realice 2^{n} operaciones antes de detenerse. Para n pequeña, digamos 100, y suponiendo, por ejemplo, que la computadora realiza 10^{12} operaciones cada segundo, el programa se ejecutará durante aproximadamente 4 × 10^{10} años, que es el mismo orden de magnitud que la edad del universo. Incluso con una computadora mucho más rápida, el programa solo sería útil para casos muy pequeños y, en ese sentido, la intratabilidad de un problema es algo independiente del progreso tecnológico. Sin embargo, un algoritmo de tiempo exponencial que toma 1.0001^{n} operaciones es práctico hasta que n sea relativamente grande.

Del mismo modo, un algoritmo de tiempo polinómico no siempre es práctico. Si su tiempo de ejecución es, digamos, n^{15}, no es razonable considerarlo eficiente y sigue siendo inútil, excepto en casos pequeños. De hecho, en la práctica, incluso los algoritmos n^{3} o n^{2} a menudo no son prácticos en problemas realistas.